Project Overview
The Weighted Portfolio Analysis tool is an implementation of Modern Portfolio Theory (MPT) principles. It allows investors to construct custom baskets of assets and simulate their combined performance over time. By adjusting the weight allocation of each asset, users can visualize the impact of diversification on volatility and total return, ultimately aiming to construct an "Efficient Frontier" where returns are maximized for a given level of risk.
Problem Statement
Investors often struggle to visualize how different asset allocations impact overall portfolio performance. A tool is needed to simulate and analyze various portfolio structures dynamically.
Strategy / Model Definition
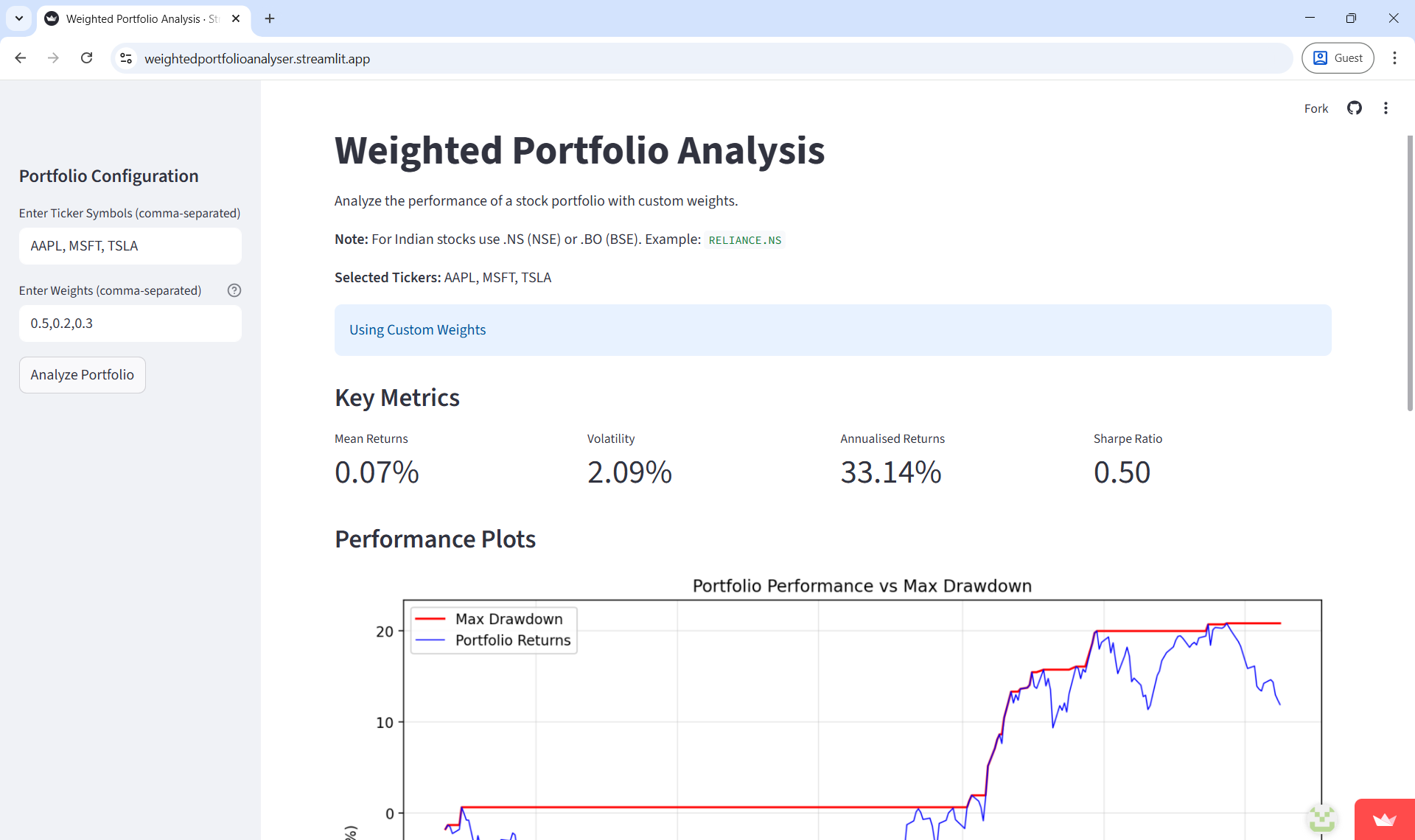
The core strategy revolves around the Weighted Sum Model. The portfolio return is calculated as the weighted average of individual asset returns. However, the portfolio volatility (risk) is not merely a weighted average; it takes into account the covariance matrix of the assets. The goal is to find assets with low or negative correlation to reduce overall portfolio variance without necessarily sacrificing returns—the essence of diversification.
Methodology
Key technologies and steps:
- Input ticker symbols and corresponding weights.
- Fetch historical price data.
- Calculate weighted returns and portfolio statistics.
Metrics & Evaluation Criteria
Evaluates Sharpe Ratio, Annualized Return, and Volatility.
Results & Observations
The analysis consistently highlights that a 100% allocation to a single high-growth stock (like NVDA) usually yields the highest absolute return, but comes with massive drawdowns (volatility). By mixing in uncorrelated assets (e.g., adding 20% Bonds or Defensive stocks), the Sharpe Ratio (Return/Risk) often improves drastically. The tool visually demonstrates that a 60/40 portfolio often provides a smoother equity curve, protecting the investor psychologically during market downturns while still capturing significant upside.
Interpretation & Limitations
While the math is solid, the model relies on historical correlation, which is not static. In times of extreme market stress (like the 2008 crash or COVID-19), correlations often converge to 1—meaning all assets fall together. Therefore, while diversification works well in normal markets, it may offer less protection during systemic liquidity crises.
Project Artifacts
Key Takeaways
"Diversification is the only free lunch in finance." This project proved that mathematically. It also emphasized that portfolio construction is a personal endeavor; there is no "perfect" portfolio, only one that matches the specific risk tolerance and time horizon of the investor.